Sunday, May 18, 2014
Polar coordinates
Polar coordinates are a way to label a point on a plane using the radius and angle, rather than x and y coordinates such as (x,y). Some important terms include: Pole=origin, polar axis=ray from the pole, r=directed distance from O to P, and lastly, Theta=angle couterclockwise from polar axis to segment OP. Unlike normal (x.y) coordinates, polar coordinates can be different yet be at the same point! What do I mean? Well, since an angle can be measured counterclockwise or clockwise, a coordinate like (r,theta) will equal (-r, theta+pi).
You should know the ways to convert coordinates from polar to rectangular. The equations you need are as follows:
You should know the ways to convert coordinates from polar to rectangular. The equations you need are as follows:
Here is an example of a conversion:
Graphs of Polar Equations
Polar Equations, as already learned, are different from rectangular equations and useful in their own ways. Polar coordinates correspond with Polar equations, which both use angles and radius. These equations can make much cooler shapes and figures that rectangular equations can not make due to its limitations. Some typical polar equations:
Polar Equations can also have symmetry and be symmetrical to many axes. One can use the symmetry test to yield what the polar equation/graph is symmetrical to. The symmetry test is as follows:
One should also use a graphing utility to check your graph or graph extremely complex equations/graphs.
Ellipses and Hyperbolas Review
Ellipses and Hyperbolas are closely related in both equations and definitions, even though they look nothing alike, so they can be easily learned together. First of all, an ellipse is the set of all points (x, y) the sum of whose distances from two distinct fixed points (foci) is constant. Some terms include: vertices=The line through the foci that intersects the ellipse at two points, major axis=The chord joining the vertices, midpoint=center of the ellipse, minor axis=The chord that is perpendicular to the major axis. Ellipse equations:
The Hyperbola is the set of all points (x, y) the difference of whose distances from two distinct fixed points (foci) is constant. The terms that were defined with the ellipse also apply to hyperbolas. Hyperbola Equations:
As you can see, they are similar in many ways such as how their equations are presented. The main differences that can be confusing and need to be memorized are the differing signs in the equations.
Vectors in Space Review
Vectors, can be associated with an animated villain or cool mathematical concept. Sadly, I will have to explain the math one. Vectors in space, unlike normal vectors, exist in a 3D field, and therefore have three coordinates that denote is position unlike vectors on a plane. A vector in space can be denoted by v= <v1,v2,v3>. This means that there are three axes in all, the x, the y, and the z.The zero vector is denoted by 0 = <0,0,0>. The unit vectors are as follows : i= <1,0,0>, j= <0,1,0>, and k= <0,0,1> in the direction of the positive z-axis. One can obtain the component form of a vector by subtracting the values of the coordinates of the starting point by the values of the coordinates of the terminal point. Equations for vectors in space are as follows:
and an example of a vector in space:
Polar Coordinates Review
Joel had taught the class about polar coordinates, a way to label a point on a plane using the radius and angle, rather than x and y coordinates. Some important terms include: Pole=origin, polar axis=ray from the pole, r=directed distance from O to P, and lastly, Theta=angle couterclockwise from polar axis to segment OP. Unlike normal (x.y) coordinates, polar coordinates can be different yet be at the same point! What do I mean? Well, since an angle can be measured counterclockwise or clockwise, a coordinate like (r,theta) will equal (-r, theta+pi).
You should know the ways to convert coordinates from polar to rectangular. The equations you need are as follows:
You should know the ways to convert coordinates from polar to rectangular. The equations you need are as follows:
Matrices and Systems of equations Review
Miss V's daughter, Kara, followed in her footsteps and taught the ways of Matrices and Systems of equations. The two ways to solve system of equations with matrices, Gaussian Elimination and Gauss-Jordan Elimination. To use these techniques, one must know Elementary Row Operations, the ways of which one can manipulate matrices to get numbers where they want. These operations include: 1) interchange any two rows 2) multiply a row by a non-zero constant 3) add one row to another.
The Gaussian Elimination with Back-Substitution method steps are as follows:
-Write the augmented matrix of the system of linear equations
-Use elementary row operations to rewrite the augmented matrix in row-echelon form
-Write the system of linear equations corresponding to the matrix in row-echelon form, and use back-substitution to find the solution
Make sure that you have a leading 1 and that the main diagonal is consisted of 1's. Everything under the main diagonal has to be zeros but above the main diagonal there can be any numbers.
The Gauss-Jordan Elimination method steps are as follows:
-Write the augmented matrix of the system of linear equations
-Use elementary row operations to rewrite the augmented matrix in row-echelon form
-Write the system of linear equations corresponding to the matrix in row-echelon form
Make sure that you have a leading 1 and that the main diagonal is consisted of 1's. Everything under and above has to be zeros.
The Gaussian Elimination with Back-Substitution method steps are as follows:
-Write the augmented matrix of the system of linear equations
-Use elementary row operations to rewrite the augmented matrix in row-echelon form
-Write the system of linear equations corresponding to the matrix in row-echelon form, and use back-substitution to find the solution
Make sure that you have a leading 1 and that the main diagonal is consisted of 1's. Everything under the main diagonal has to be zeros but above the main diagonal there can be any numbers.
The Gauss-Jordan Elimination method steps are as follows:
-Write the augmented matrix of the system of linear equations
-Use elementary row operations to rewrite the augmented matrix in row-echelon form
-Write the system of linear equations corresponding to the matrix in row-echelon form
Make sure that you have a leading 1 and that the main diagonal is consisted of 1's. Everything under and above has to be zeros.
Cross Product Review
The two main ways to find the cross products are using determinants/cofactors, and the quicker method without cofactors. In the determinants/cofactors method, you must use cofactor expansion where the values of the vectors are placed in a determinant and then expanded into cofactors for addition. An example can be seen below:
Another method is by using the determinant also, but by using the quick method without cofactors, but by copying the first two columns to the right so one can multiply diagonally while adding or subtracting the values. You add when the multiplication is done from a top, left to a down, right while you subtract when it is from a down, left to a top, right. One can learn many things through the dot products such as how lluxvll equals the area of a parallelogram. Another important thing is the triple scalar product, which can only be found out when there are three vectors in space. The triple scalar product can be used to find the volume of the 3D shape the vector forms from one side.
An example of the shortcut method can be seen below:
Another method is by using the determinant also, but by using the quick method without cofactors, but by copying the first two columns to the right so one can multiply diagonally while adding or subtracting the values. You add when the multiplication is done from a top, left to a down, right while you subtract when it is from a down, left to a top, right. One can learn many things through the dot products such as how lluxvll equals the area of a parallelogram. Another important thing is the triple scalar product, which can only be found out when there are three vectors in space. The triple scalar product can be used to find the volume of the 3D shape the vector forms from one side.
An example of the shortcut method can be seen below:
Bionomial Theorem Review
Jacqueline had re-taught the class the binomial theorem/expansion. In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. There are also two main ways to find out the binomial coefficients of an expansion. The main way that we had normally used was with Pascal's triangle, a triangle of numbers that can be used to find the coefficients of a binomial expansion, where the row number correlates with the power. With this pascal triangle, individual terms can also be found easily with the knowledge of the coefficient that corresponds to the specific term. The binomial theorem is as follows.
Tuesday, May 6, 2014
Parametric equations
Parametric equations are basically normal x and y equations with the addition of a third variable, t. With this thrid variable, one can learn another useful item that corresponds eith the change of x and y such as time. To eliminate the parameter, first start with the parametric. Then, solve for the variable t in one of the equations given. After that, substitute the value of t that was found into the second equation. Lastly, move around values to obtain the rectangular equation, or normal x and y equation. To eliminate the parameter, you can also create a graph by creating a table of values that contain the values of all three variables.
Bernoulli's equation
Finding out the pressure of water in a pipe can be extremely hard and tiring, but it can even harder to find out the pressure of more than one place in the pipe! However one can actually easily do this with an equation! With bernouilli's equation "p+1/2pv^2+pgh", which is constant for any two points in a pipe or any other water filled container, one can easily find out the balance between pressure, velocity, and height, and therefore, easily find out the pressure. With this one equation, one can also learn that as area increases, pressure decreases! This equation and many others that involves physics or other math-related subjects, one can understand the world more deeply. This shows that a single equation can be extremely useful and versatile.
Cross Product of Vectors
There are many ways to find the cross product of vectors. This includes using the determinant form. In this method, you must use cofactor expansion where the values of the vectors are placed in a determinant and then expanded into cofactors for addition. An example can be seen below:
Another method is by using the determinant also, but by using the quick method without cofactors, but by copying the first two columns to the right so one can multiply diagonally while adding or subtracting the values. You add when the multiplication is done from a top, left to a down, right while you subtract when it is from a down, left to a top, right. One can learn many things through the dot products such as how lluxvll equals the area of a parallelogram. Another important thing is the triple scalar product, which can only be found out when there are three vectors in space. The triple scalar product can be used to find the volume of the 3D shape the vector forms from one side.
Vectors in Space
In mathland, we had reviewed the concept of vectors, but with a twist. With vectors in space, there are three numbers to denote the vector due to the the ammount of directions it goes. A vector can be written as <V1, V2, V3>. This means that there are three axes in all, the x, the y, and the z. One can obtain the component form of a vector by subtracting the values of the coordinates of the starting point by the values of the coordinates of the terminal point. All in all, vectors in space are just normal vectors with one more direction/value. One can use the normal equations for vectors on a plane with the addition of the third value into the equation according to how the Xs and Ys are presented in the equation. These equations include the vector length, unit vector, vector addition, and etc.
Math Genius
A man who was attacked and beat up, suddenly becomes a math genius! How did this happen? Well, due to his brain injury, this man became a savant, an individual who is exceptional in one or a few areas of cognition. This one injury can help everyone learn how they might also become better mathematicians! As shown through measuring his brain waves and activity, math skills resides mostly in the left hemisphere of his brain. This man now sees the world through mathematical concepts such as geometry. I hope that we can figure out soon how we all can quickly and easily increase our math skills. With the way human technology has been progressing, I would not be surprised at all if the use of surgery to increase skills was available in my lifetime. One can learn more here : http://www.huffingtonpost.com/2014/05/06/brain-injury-jason-padgett-math-genius_n_5273609.html
Limits Introduction
In mathland, we had learned about limits, a concept that is used mainly in calculus. However, we still learned the basics of limits. Limits are basically the values that equations that are functions or sequences approach. To find a limit, one can apply graphing or just create a table where the values close to the x value that the function goes to can be known. Through this method with the table, an approximation can be made for the value of the limit. An example of each method is shown below.
Evaluating limits
Today in Mathland, we learned avout something that will help us later in Calculus. we learned about how to evaluate limits. There are three main steps to it. First, you must direct substitute to see if you get 0/0. If you do not, that will be your limit. Next, you do cancellation or rationalization. You do rationalization if there is a square-root. Next, you would direct substitute to get the answer. Here are a few examples.
There can also be one- sided limits. This is true for when there are gaps in the graph. This can be seen in the following picture.
Friday, March 21, 2014
Fun math
Learning and teaching math can be fun too! Just like this teacher in indianapolis: http://fox59.com/2014/03/20/indianapolis-teacher-uses-march-madness-to-teach-geography-math/#axzz2wc0QGxwY, math problems does not need to involve only problems where a person buys 100 watermelons or plots out his/her garden. This particular teacher had involved the use of the March madness or playoff time for college basketball to teach his math students. He uses th brackets for the students to find things such as means, medians, and modes. All math teachers should do something like this!
Thursday, March 20, 2014
Rotation of Conics
When you have Bxy or another constant with xy in an equation, you have to change it to the form of 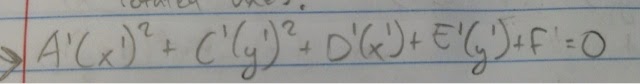 . To do this, you must use the following equations:
. To do this, you must use the following equations: 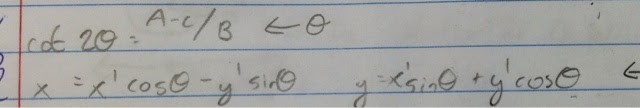 . The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated.
. The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated.
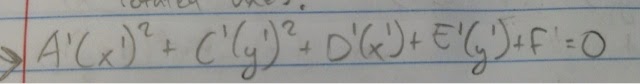 . To do this, you must use the following equations:
. To do this, you must use the following equations: 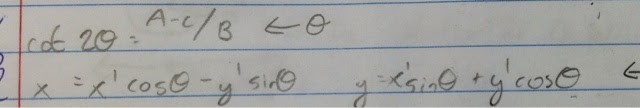 . The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated.
. The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated. Hyperbolas
Hyperbolas are basically, in definition, the set of all points (x,y) the difference of whose distances from two fixed points called the foci is always constant. The only difference between the definition of a hyperbola and an ellipse is that hyperbolas the distances from the foci and a point on the hyperbola is fixed while is the sum of the distances between foci and a point on the ellipse is fixed. There two branches of a hyperbola. Vertices are the points of a hyperbola where the line through the two foci intersects a hyperbola. The transverse axis is the line segment that connects the vertices. The exact midpoint on the transverse axis is the center of a hyperbola.
Below are the equations to a hyperbola:
Sunday, March 16, 2014
Death Probability
As humans, we try to survive and live as long as we can possibly can! However, there are many things that are harmful to us and can kill us. These things include drowning and diseases! Using math, we can find out the probability of how some things might kill us so can try to prevent or avoid it. For example, there is a 1-5 chance that we can die due to a heart disease. You can find out the 25 highest possibilities that can cause human deaths in the following website: http://list25.com/the-25-most-likely-ways-you-will-die/2/. Hope we all live long!
Probability
Many people use probability, the chance that something will occur, on daily basis! It is how most people decide to do things. For example, one would probably not walk on a plank that has a high probability of breaking under your weight! Therefore, it is important to know probability and how to find them. Basically, probability is the number of successful outcomes over the number of total outcomes.However, there are also many scenarios concerning probability and equations that go with them. Here are the equations: 
Mainly, you should know the ones for independent, dependent, complement, and classical probability formulas. Permutations and Combinations are also important when you are finding the amount of ways something can occur.
Mainly, you should know the ones for independent, dependent, complement, and classical probability formulas. Permutations and Combinations are also important when you are finding the amount of ways something can occur.
Measures of Central Tendency
There are many measures of central tendency that are used when we are exploring data. For example, there is the mean. The mean is basically the average which can be found by adding all the values up and then dividing by the amount of numbers. Then, there is the median which is the number that is exactly in the middle. The mode is the number that occurs most often. There are also measures of dispersion. One is the variance which can be obtained by the equation: 
The square-root of the variance is the standard deviation. Also, there are quartiles when exploring data. The lower quartile is the median of the numbers before the median of all numbers, and the upper quartile is the median of the numbers after the median of all numbers.
The square-root of the variance is the standard deviation. Also, there are quartiles when exploring data. The lower quartile is the median of the numbers before the median of all numbers, and the upper quartile is the median of the numbers after the median of all numbers.
PI
Pi, the mathematical constant that is so important to many mathematical concepts and mathletes, is namely irrational and goes on forever. Most people know that it starts with 3.14159 and goes on forever from that point, but how do we know that that this number is correct? There have been many mathematicians such as Niven and Cartwright who have written proofs for pi with many funky concepts and weird equations which you can see for yourself here: http://en.wikipedia.org/wiki/Proof_that_%CF%80_is_irrational. One can also learn about why pi is 3.1459 here where things are easier to understand: http://www.slideshare.net/yaherglanite/estimating-pi. Basically, all you need to know is that the contant is true and that it works though! Trust it
Ellipses
Ellipses are bascially weirdly shaped circles, but in a proper definintion, it is the set of all points (x,y) the sum whose distances from two distict fixed points called the foci are always constant. An ellipses has both vertices and axes. The vertices are the points where a line through the foci would pass through on the sides of an ellipse. The chord that connects these vertices is called the major axis. The minor axis is the chord that is perpendicular to the major axis and connects through the center or midpoint which is, as the name states, at the center or midpoint of the ellipse.
Here is a picture of an ellipse with its major parts:

Here is the equation for an ellipse:

Here is a picture of an ellipse with its major parts:
Here is the equation for an ellipse:
Parabolas
We had learned in Mathland about the Parabolas, which are in definition, the set of all points (x,y) that are equidistant from a fixed line or directrix and a fixed point that is not on the line called a focus. The two main equations for a parabola are: (x-h)^2=4p(y-k) for vertical parabolas and (y-k)^2=4p(x-h) for horizontal parabolas. The directrix for the vertical one is y=k-p while the one for the horizontal is x=h-p. Mainly, for problems concerning the parabola, you will either find the focus, directrix, or equation for the parabola. To do this, it is easier to first try to draw it out!

Here is a picture of a parabola with a focus and a directrix:
Thursday, February 27, 2014
Pascal's Triangle
One can use the Binomial Theorem or the Pascal Triangle to expand and equation such as (2x+3y)^4 without just multiplying it all out manually! However, as Miss V quietly states, Pascal's Triangle is the one that a person should use. With the Pascal's triangle method, you find the row according to the power of your equation. Then, you fill in the number after each constant starting with the highest power of the first term and descending and the lowest number of the second term and ascending after each term in your expansion. With the use of the Pascal's Triangle, one can also find the term that Combinations are trying to find by looking at the first number before the C for the row number and the number after the C for the term. However, you must subtract 1 to the term number to get the correct answer.
Here is a Pascal Triangle:
Here is a Pascal Triangle:
Mathematical Induction
In Mathland, we learned about how we can prove a statement using the platform of Mathematical induction. Mathematical induction is very simple, but is long and has clear steps and things you must write every time for it to hold true! For example, without the statement: "assume the statement is true for n" at the start of step 2, it would not hold true! With mathematical induction, you must memorize the format in order to do it. Mainly, there are two steps. The first step is prove the statement is true at the starting point while step 2 is to assume the statement is true for n and then prove that the statement is true for n+1.
Here is a picture of the format you must follow, the orange parts hold three for all mathematical induction proofs
Here is a picture of the format you must follow, the orange parts hold three for all mathematical induction proofs
Well Ordering Principle
Basically, the Well Ordering Principle or Well-ordering theorem is a term in Math that within a set of positive integers, there are is a least element, which is self-explanatory for it is the number that is the least in value. this principle turns out to be logically equivalent to the mathematical induction, the fifth axiom of Peano, which is quite surprising. If mathematical induction is true for all natural numbers, then so is the well-ordering principle. Basically, the well-ordering principle can be proved with the mathematical induction. Ultimately, both imply each other to work because they are based on the same type of logic.
Here is an the proof of well-ordering principle according to mathematical induction: the http://www.math.wustl.edu/~chi/310notesIV.pdf
Here is an the proof of well-ordering principle according to mathematical induction: the http://www.math.wustl.edu/~chi/310notesIV.pdf
Thursday, February 20, 2014
0!
Most factorials are easy to understand and to find the solution to, except the factorial of a certain number. This number is 0. It is weird that every other number above zero is basically that number multiplied by all numbers below it towards one. However, 0 x 0 should be zero for even if it is multiplied by one, it is still zero. However, through this article, one can basically understand why mathematicians had defined 0! As 1. One huge reason is due to permutations. A set with no values should be arranged in only one way. Also, the formulas for permutations and combinations need the value of zero factorial to be one so that it is consistent with the equations that are derived. It is basically made up so that math equations stay true. One can learn more from this article: http://statistics.about.com/od/ProbHelpandTutorials/a/Why-Does-Zero-Factorial-Equal-One.htm
Arithmetic Sequences
We learned about arithemetic sequences. Arithmetic sequences are sequences of numbers where there is a common difference between each number such that a number is is being added to each number to get the next number in the sequence. There are both explicit and sum formulas. Explicit formulas are used to find a single number in a sequence when the first number and the change or common difference between each number is known. The sum formulas are used to find the sum of the whole arithmetic sequence when the first and last number and the amount of numbers are known. The equations and examples will be in a picture below.
Sequences and Summation
In Mathland, we learned about sequences and summation. A sequence can be infinite and or finite and that appellation pretty much sums up how they are. Numbers with an exclamation mark can also be known as factorials. A factorial is basically the number that is being factorized times all the integers lower than it to zero. For example: 4!=4x3x2x1. However, the factorial of zero is one due to some important reasons. Summation notation is a way one can sum up sequences when the upper limit, explicit formula, and lower limit are known. There are also many properties of summation notations. Below are summations notations and their properties.
Thursday, February 13, 2014
Determinants
This was my group's educreation video on how to use determinants:
http://www.educreations.com/lesson/view/p-635-36/16782864/?s=RdR6UY&ref=app
http://www.educreations.com/lesson/view/p-635-36/16782864/?s=RdR6UY&ref=app
Website
This was my group's website:
https://sites.google.com/a/maranathastudents.org/mathlandgroup5/
https://sites.google.com/a/maranathastudents.org/mathlandgroup5/
Equation of a Line with Determinants
This was my group's voicethread: https://voicethread.com/?#q.b5437871.i27642718
Thursday, February 6, 2014
Cryptography
Inverses of Matrices
Today in Mathland, we learned about how to make inverses of matrices. An in inverse of a matrix or (A^-1) when multiplied to the matrix it is an inverse of or (A) becomes an identity matrix of the same dimensions. They can be multiplied in any order. The steps to do this includes:
1) link the matrix you want to make an inverse of with an identity matrix of the same dimensions
2) use matrix rules to manipulate the matrix so that the left side becomes the identity matrix while the right becomes an inverse matrix.
3) then you can multiply the inverse with its inverse to see if it makes an identity matrix.
If the left side of the bottom row becomes all zeroes, it is a singular matrix with no inverse matrix. Below, i have examples of both normal and matrices with no solution: (the first one is singular and has no solution while the second one is normal and has a solution)
Matrices Solutions
Hello guys, today I will be explaining when a matrix has solutions and when they have infinite solutions! First of all, a matrix that has no solution will have a row with zeroes in it from the left until it reaches a non-zero number on the far right(the number that is separated by a line. This makes sense because if we put that row in an equation form, 0=a number that is not zero and that is not possible! On the other hand, a matrix that has infinite solutions is one where there are less rows than columns. This means that there will be less equations than variables! To solve theses kinds of problems, we will have to solve in terms of a variable which makes the possibilities infinite! By the way, The row echelon form of a matrix is when it is set up a specific way where the main diagonal in the matrix will only consist of 1's and the numbers surrounding that will all be 0's. Good luck everyone!
Thursday, January 30, 2014
Mathematical Intuition
Math is a crucial topic to any child who wants a good educationa and future. Then how can a child improve in mathematics? Well, through the use of psychology and experiments, some people have found out that there is a link between kids who practiced intuition with math. This means that kids that are exposed to mathematics and practice to think unconciously about numbers and ammounts by actions such as guessing ammounts, are more likely to do better in math at school. This was experimented on by psychologists, and this link can clearly be seen through some of their designed experiments. Learn more about this in this article: http://psychcentral.com/news/2014/01/30/intuitive-training-improves-math-scores/65193.html
Matrices
1) interchange rows
2) add a row to another row
3) multiply or divide a row by a constant
The main goal of the Gaussian way is to get zeros below a diagonal of ones that start from the top left corner and end in the bottom right corner. Then, you create equations from the numbers you have and use back substitution into each equation to gain the values of each variable. However, in the Gaussian methods, zeroes are wanted everywhere except in the aforementioned diagonal. With the Gaussian, there is no need to find or use equations and substitution. all you need to do is state the value of each variable from interpreting the matrix.
Trigonometric Identities Review
We had learned about the trigonometric identities beforehand, but we never actually memorized them all! In a lesson this week, we learned that we need to memorize all forty eight! We have started slow with practicing the 11 fundamental ones on a worksheet, but we will gradually have to review more. The identities will help us all in many ways in Calculus if we choose to take it next year. The identities help us manipulate equations concerning angles to the simplicity or complexity that we desire. It will be invaluable for students in calculus next year because they will be able to do problems way faster and easier. Below, I have a picture of most of the identities:
Wednesday, January 22, 2014
Math problems
It has been discovered in Seattle that problems in mathematics had started even before kindergarten! They had learned that students who are entering kindergarten lacked the necessary skills for success in mathematics in the school. It was done by an assessment of their abilities in the many parts of their academics, including math. This means that kids did not receive enough exposure to math before school starts. This probably explains why students in Seattle and other states may lack math skills later on in higher levels of education including middle school and high school. With further studies, we may learn why math maybe lacking the states compared to other nations and a solution can be provided.
http://blogs.seattletimes.com/educationlab/2014/01/22/math-struggles-start-even-before-kindergarten-state-says/
Tuesday, January 21, 2014
Non-Square System
A topic that most people in my class are shaky one is the non-square sytem. In non-square systems, there are more variables to solve for than there are equations that are given. For example, there might be three variables including x, y, and z, while there is only two equations. This means that we have to solve the variables in terms of Z or another common variable, but in this class, we will use Z. Therefore, in this scenario, x and y will both equal some form of Z (for example, y=5z and x=z+7). Then you will put the answer in terms of "a" instead of z. In this step, you will just replace z with "a" in the answer.
Below, is an example Miss V did for review for a non-square system: in this scenario, there was two equations with 3 variables present.
Thursday, January 16, 2014
The Birthday Problem
The birthday problem is an interesting mathematical phenomenon/equation. It shows the probability of two or more people sharing the same people in a room full of n amount of people. This equation is actually more interesting than people think! One would assume that there needs to be more than 365 people (or at least i would), but it is far less. In fact, there only needs to be 100 people for there to be a 99.99997 percent of two people sharing the same birthday! This is extremely interesting to me for it is not something i would try to figure out at all before finding out there is an actual equation for it! It is cool that someone actually took alot of time to figure this out.
www.youtube.com/watch?v=qRLVcr-pk5I
Partial Fraction Decomposition
The steps to Partial Fraction Decomposition include:
1) multiply
2) distribute
3) collect like terms
4) factor
5) equate
6) solve
Below, i have examples:
As shown in the examples, there are also many ways the partial fraction decomposition can be aet up according to the denominator of the initial fraction. 3 different ways are shown below
Linear Programming
Today in Mathland, we actually learned something quite usefull. Ms.Vanspronsen even stated that her friend did this for a living. Linear programming is done to find things such as maximum and minimum profit from a system of inequalitites. There are seven steps in all which may take up quite some time. Linear programming is used in businesses' such as wheat farms to find out what they should produce and how much of each quantity. For example, one company can find out how much pool tables and air hockey tables they should make with the amount of time they have. This same example is shown below:
Subscribe to:
Comments (Atom)




























