Friday, March 21, 2014
Fun math
Learning and teaching math can be fun too! Just like this teacher in indianapolis: http://fox59.com/2014/03/20/indianapolis-teacher-uses-march-madness-to-teach-geography-math/#axzz2wc0QGxwY, math problems does not need to involve only problems where a person buys 100 watermelons or plots out his/her garden. This particular teacher had involved the use of the March madness or playoff time for college basketball to teach his math students. He uses th brackets for the students to find things such as means, medians, and modes. All math teachers should do something like this!
Thursday, March 20, 2014
Rotation of Conics
When you have Bxy or another constant with xy in an equation, you have to change it to the form of 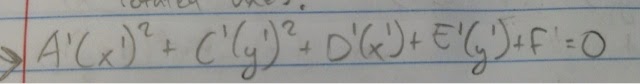 . To do this, you must use the following equations:
. To do this, you must use the following equations: 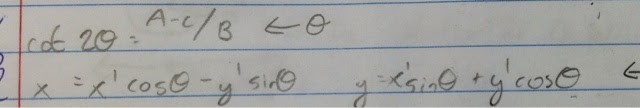 . The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated.
. The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated.
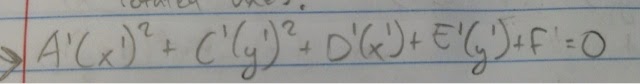 . To do this, you must use the following equations:
. To do this, you must use the following equations: 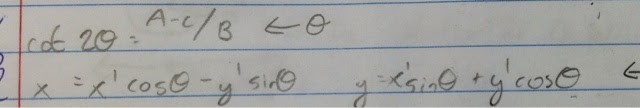 . The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated.
. The steps to change the equation includes first finding the angle. Then in step 2, you find the new x and y. Then, you plug it into the original equation. Lastly, you graph the rotated conic. These steps may be long and uses alot of hardcore algebra skills. Don't make a mistake! Here is an example of one changed equation according to the way it was rotated. Hyperbolas
Hyperbolas are basically, in definition, the set of all points (x,y) the difference of whose distances from two fixed points called the foci is always constant. The only difference between the definition of a hyperbola and an ellipse is that hyperbolas the distances from the foci and a point on the hyperbola is fixed while is the sum of the distances between foci and a point on the ellipse is fixed. There two branches of a hyperbola. Vertices are the points of a hyperbola where the line through the two foci intersects a hyperbola. The transverse axis is the line segment that connects the vertices. The exact midpoint on the transverse axis is the center of a hyperbola.
Below are the equations to a hyperbola:
Sunday, March 16, 2014
Death Probability
As humans, we try to survive and live as long as we can possibly can! However, there are many things that are harmful to us and can kill us. These things include drowning and diseases! Using math, we can find out the probability of how some things might kill us so can try to prevent or avoid it. For example, there is a 1-5 chance that we can die due to a heart disease. You can find out the 25 highest possibilities that can cause human deaths in the following website: http://list25.com/the-25-most-likely-ways-you-will-die/2/. Hope we all live long!
Probability
Many people use probability, the chance that something will occur, on daily basis! It is how most people decide to do things. For example, one would probably not walk on a plank that has a high probability of breaking under your weight! Therefore, it is important to know probability and how to find them. Basically, probability is the number of successful outcomes over the number of total outcomes.However, there are also many scenarios concerning probability and equations that go with them. Here are the equations: 
Mainly, you should know the ones for independent, dependent, complement, and classical probability formulas. Permutations and Combinations are also important when you are finding the amount of ways something can occur.
Mainly, you should know the ones for independent, dependent, complement, and classical probability formulas. Permutations and Combinations are also important when you are finding the amount of ways something can occur.
Measures of Central Tendency
There are many measures of central tendency that are used when we are exploring data. For example, there is the mean. The mean is basically the average which can be found by adding all the values up and then dividing by the amount of numbers. Then, there is the median which is the number that is exactly in the middle. The mode is the number that occurs most often. There are also measures of dispersion. One is the variance which can be obtained by the equation: 
The square-root of the variance is the standard deviation. Also, there are quartiles when exploring data. The lower quartile is the median of the numbers before the median of all numbers, and the upper quartile is the median of the numbers after the median of all numbers.
The square-root of the variance is the standard deviation. Also, there are quartiles when exploring data. The lower quartile is the median of the numbers before the median of all numbers, and the upper quartile is the median of the numbers after the median of all numbers.
PI
Pi, the mathematical constant that is so important to many mathematical concepts and mathletes, is namely irrational and goes on forever. Most people know that it starts with 3.14159 and goes on forever from that point, but how do we know that that this number is correct? There have been many mathematicians such as Niven and Cartwright who have written proofs for pi with many funky concepts and weird equations which you can see for yourself here: http://en.wikipedia.org/wiki/Proof_that_%CF%80_is_irrational. One can also learn about why pi is 3.1459 here where things are easier to understand: http://www.slideshare.net/yaherglanite/estimating-pi. Basically, all you need to know is that the contant is true and that it works though! Trust it
Ellipses
Ellipses are bascially weirdly shaped circles, but in a proper definintion, it is the set of all points (x,y) the sum whose distances from two distict fixed points called the foci are always constant. An ellipses has both vertices and axes. The vertices are the points where a line through the foci would pass through on the sides of an ellipse. The chord that connects these vertices is called the major axis. The minor axis is the chord that is perpendicular to the major axis and connects through the center or midpoint which is, as the name states, at the center or midpoint of the ellipse.
Here is a picture of an ellipse with its major parts:

Here is the equation for an ellipse:

Here is a picture of an ellipse with its major parts:
Here is the equation for an ellipse:
Parabolas
We had learned in Mathland about the Parabolas, which are in definition, the set of all points (x,y) that are equidistant from a fixed line or directrix and a fixed point that is not on the line called a focus. The two main equations for a parabola are: (x-h)^2=4p(y-k) for vertical parabolas and (y-k)^2=4p(x-h) for horizontal parabolas. The directrix for the vertical one is y=k-p while the one for the horizontal is x=h-p. Mainly, for problems concerning the parabola, you will either find the focus, directrix, or equation for the parabola. To do this, it is easier to first try to draw it out!

Here is a picture of a parabola with a focus and a directrix:
Subscribe to:
Comments (Atom)

